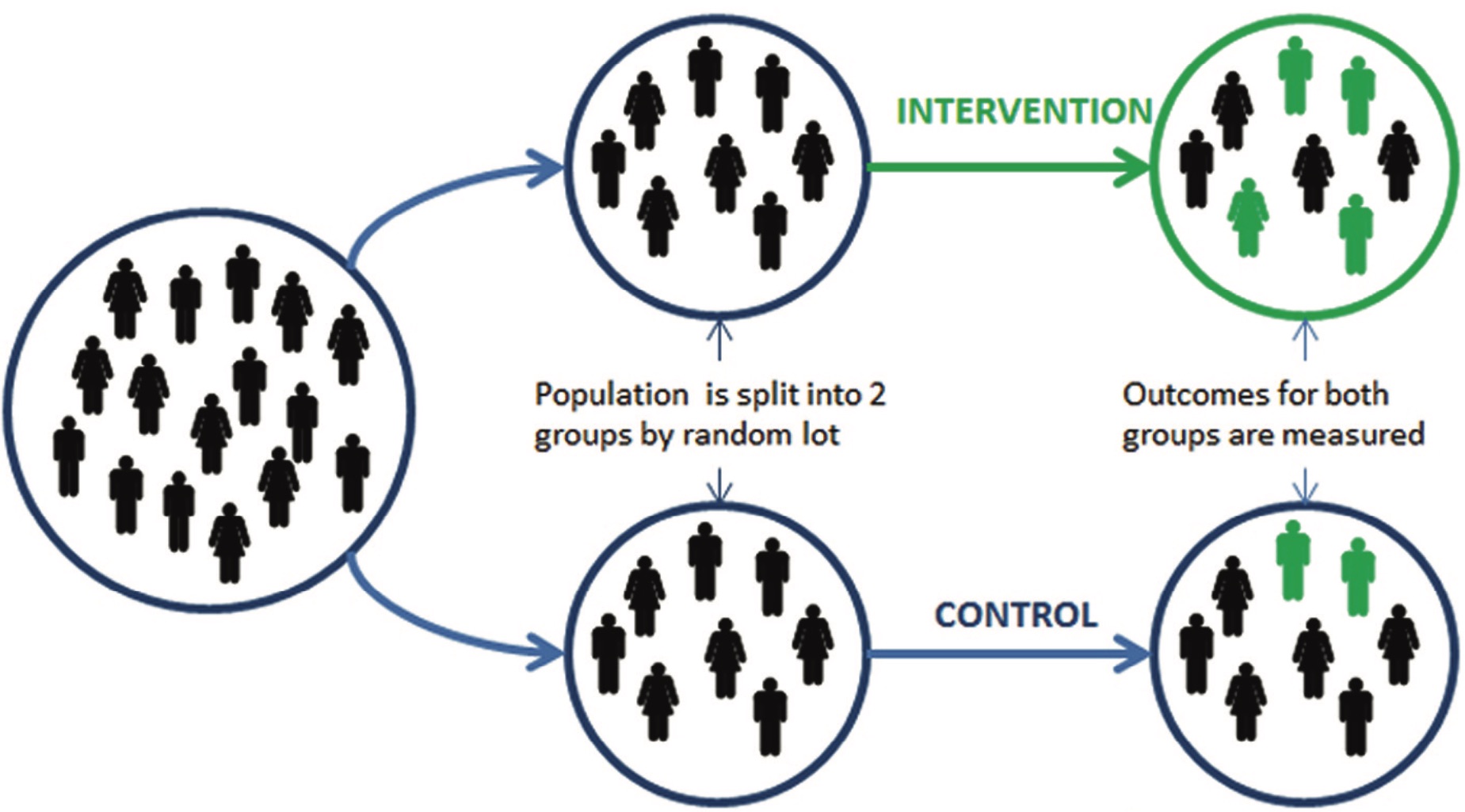
17 Random assignment

In its simplest form, randomised trials work by splitting trial participants into two or more groups by random lot. Each group is then given a different intervention, with one of those groups typically a “control group” or “test group” that receives no intervention or the status quo.

Groups might be allocated randomly by drawing numbers out of a hat, flipping a coin or, more commonly in experimental work, using a pseudo-random number generator. It is not the experimenter that decides who gets an intervention or not, but rather chance.

Randomisation works as a control technique because it enables experimenters to hold approximately equal the sources of experimental bias, such as uncontrolled variables, between the control and treatment groups. These might even be variables of which we are ignorant.

In Uncontrolled: The Surprising Payoff of Trial-and-Error for Business Politics and Society, Jim Manzi (2012) gives the following example:

[S]uppose researchers in 1950 wanted to test the efficacy of a pill designed to reduce blood pressure but did not know that about 10 percent of the human species has a specific gene variant that predisposes them to adult-onset hypertension. If the researchers selected 3,000 people, and randomly assigned 1,500 to a test group who are given the pill and 1,500 to a control group who received a placebo, then about 150 patients in each group should have the gene variant of interest (though the researchers would have no explicit information about this and wouldn’t even have thought to investigate it). Therefore, when these researchers compared the change in blood pressure before and after taking the pill for the test group versus the control group, their estimate would not be biased by a much higher proportion of patients with the gene variant of interest in one group or the other

Randomisation relies on the law of large numbers, the idea that as sample size increases the sample average converges to the expected value. In the case of the experiment to reduce blood pressure, as the size of the groups increased, we would expect the proportion of people with the hypertension genetic variant to converge to around 10% in each group.

To think of what that means intuitively, if you had only ten in each group, there is a material chance the groups could have zero, one, or more people with the hypertension variant, although it would rarely be three or more. Therefore, with a small sample, the relative proportions of the variant vary markedly between groups. It is only be collecting large samples that we can expect the groups to approximately equal proportions.

After randomisation and application of the treatment, outcomes are then measured for each group. Within certain statistical parameters (also to be covered later in this unit), we can then take the differences between the two groups to be as a result of the different interventions we received. The treatment “caused” the differences, although as noted above, we may not understand the mechanism.

You can read more about why we randomise in Glennerster and Takavarasha (2013b).

17.1 What is involved in practice?

In practice, random assignment includes the following steps:

Define those eligible for a program.
Decide the level of randomisation (such as individuals, communities, schools, call centres, bank branches). When you design a randomized evaluation, you need to decide whether to randomise individuals in and out of the program or to randomise the whole group in and out of the program.
Power Analysis: Decide the sample size.
Randomly assign which units (individuals or groups) are in the treatment, and the control group. Groups might be allocated randomly by drawing numbers out of a hat, flipping a coin or, more commonly in experimental work, using a pseudo-random number generator. It is not the experimenter that decides who gets an intervention or not, but rather chance.

We will cover some of these steps, such as power analysis, in more detail later in these notes.

17.2 Random sample versus random assignment

In both random assignment and random sampling, we use a random process to select units (individuals, households, schools, etc.). But there is a crucial difference.

In random sampling, we take a population and use a random process to select units and create a group that is representative of the entire population. We can then measure the characteristics of this group and infer from them the characteristics of the entire population. (Most surveys use this approach.)

In random assignment, we take a study population—a pool of eligible units—and use a random process to assign units to different groups, such as treatment and comparison groups (i.e., we use it to determine access to a program).

Random assignment:

Units (people, schools, etc.) are randomly assigned to different groups (e.g. treatment and comparison).
Creates two or more comparable groups.
Basis of randomised evaluation.

Random sampling:

Want to measure the characteristics of a group (e.g. average height).
Measure a random sample of the group.
Often used during randomised evaluations, especially group level randomisation.

17.3 What can be randomised?

There are three basic ways in which a program can be randomised.

Access

We can choose which people are offered access to a program. This is the most common way to randomise.

For example: “Draw a list of 200 eligible branches and then randomly select 100 to receive the new product.”

Timing

We can choose when people are offered access.

Sometimes, everyone needs access to the program (e.g. by law, fairness). We can randomly assign the time when people get access to the program.

For example, suppose a new medical treatment is proposed. Group A could get the treatment in Year 1, Group B in Year 2 and Group C in Year 3. Groups B and C are control groups in Year 1. Group C is a control group in Year 2.

Phase-in designs may result in “anticipatory effects”. The anticipation of treatment may affect the behaviour of the control group, leading to an overestimate or underestimate of the impact.

For example, consider a program that provides a laptop to each student at schools. Suppose some parents of children in the control group that planned to purchase a home computer before the evaluation decided not to purchase it and wait for their child to receive a laptop. This behavioural change is important: some parents in control group behaved differently than they would have if the program did not exist. They are no longer the best representation of the counterfactual.

Another implication of phase-in designs is that, since the control group receives treatment after a fixed time frame, there is a limited time over which impact can be measured. The evaluation of the program’s impact will be of short-term outcomes.

Encouragement

We can choose which people are encouraged to participate

Encouragement might be a small incentive, a letter, or a phone call that reminds people of their eligibility and details the steps to enrol in the program. Messaging is a form of encouragement design.

Encouragement is useful to evaluate a program already open to all eligible recipients, but only some are currently using it. Effective encouragement leads to higher take-up of the program in the treatment group than in the control group.

It is important to note that the impact of receiving encouragement to take up the program is evaluated (and its indirect effect on program take-up), rather than the direct impact of the program itself.

When studying the program’s impact, comparing the entire treatment group to the entire control group is important. When analysing the results, individuals in the treatment group who receive encouragement but do not apply for the program must still be considered a part of the treatment group. Similarly, individuals in the control group who apply for the program without special encouragement must remain in the control group for analysis.

Encouragement designs attract the following considerations:

The program to be evaluated must be undersubscribed.
To generate impact estimates, the encouragement must induce significantly higher take-up rates in the treatment group compared to the control group.
The encouragement should not have a direct effect on the outcome.
Everyone must be affected by the encouragement incentive in the same direction. If the encouragement itself increases the take-up of some groups and reduces the take-up of others, impact estimates will likely be biased.

You can read more about how to randomise in Glennerster and Takavarasha (2013a).

17.4 Opportunities to randomise

Glennerster and Takavarasha (2013a) listed ten of the most common opportunities to randomise:

New program design: A problem has been identified, and a new solution is required. This might provide an opportunity to contribute to the program design and then test.
New programs: When a program is new, and its effects are unknown, a randomised evaluation is the best way to estimate its impact.
New service: When an existing program offers a new service, rollout of the new service can be randomised.
New people: Programs often expand by adding new people. When there are not enough resources for everyone, randomising may be the fairest way to decide who will be served first. For example, Oregon had limited funding to extend Medicaid (health insurance for low-income people) to more people. They held a lottery to decide who would be offered the service.
New locations: Programs often expand to new locations. People in the new location may be added progressively through randomisation.
Oversubscription: When demand outstrips supply, random assignment may be the fairest way to choose participants. The government in Colombia uses a lottery to decide who receives secondary school tuition vouchers. The US government uses a lottery to decide who receives vouchers for housing in more affluent neighbourhoods.
Undersubscription: When the take-up of a program is low, we can increase demand by encouraging a random group. For example, a large American university encourages some employees to attend an information session on their retirement savings program.
Rotation: If people take turns accessing the program, the order in which program resources rotate can be decided randomly, with the group on rotation serving as the treatment group. If we do this, we need to consider effects lingering after the program has rotated to another group.
Admission cutoffs: Some programs have admission cutoffs. Those just below the cutoff could be randomly admitted. For example. if a bank approves loans to applicants with a credit score above 60, a random selection of applicants with scores between 55 and 59 could be approved. Those with scores in that range but not approved would form the control group.
Admission in phases: If resources are going to grow, people may be admitted to the program as resources become available.

17.5 Level of randomisation

A question that you might need to consider is the level of randomisation. Do you randomise individuals, or do you cluster? In cluster randomisation, groups of subjects are randomised. For example, if you have 20 call centres, randomise those 20 into the treatment and control rather than individual call centre staff.

Cluster randomisation can introduce greater complexity into the analysis, including potential intracluster correlation that should be accounted for. Glennerster and Takavarasha (2013a) identify considerations as to the appropriate level of randomisation as including:

Unit of measurement: What is the unit at which your outcomes will be measured? Randomisation cannot occur at a lower level than our measured outcome. For example, we need to randomise at the firm (not the worker) level to study the effect of worker training on firm profits.
Spillovers: Are there spillovers in that the intervention changes outcomes for those not directly participating? Do we want the impact estimate to capture them? Do we want to measure them? Cluster randomisation is used to control for contamination across individuals, as a change in behaviour in one might change the behaviour of others. For example, suppose you are implementing a trial to improve on-time tax return submissions by phoning taxpayers. You want to test what scripts and tools for call centre staff most effectively increase on-time submission. If you randomise at the staff–member level, staff in the control group may become aware of other approaches in their centre and change their behaviour.
Attrition: Attrition is when we cannot collect data on all our sample. Which level is best to keep participants from dropping out of the sample? For example, sometimes providing benefits to a person but not their neighbour is considered unfair. If people feel a study is unfair, they can refuse to cooperate, leading to attrition. Randomising at a higher level can help.
Compliance: compliance is when all those in the treatment group get the program and all those in the comparison don’t. Which level is best to limit departures from the study protocol? For example, if iron supplements are provided to one family member, what if they share with others? They would receive less than intended and the other family member more.
Statistical power: Statistical power is the ability to detect an effect of a given size. Which level gives us the greatest probability of detecting a treatment? Cluster randomisation reduces power by effectively reducing the sample size.
Feasibility: Which level is ethically, financially, politically and logistically feasible?
- Ethics: Randomising at an individual level may create tensions that lead to harm if some are seen as unfairly chosen. Randomising at the group level raises issues about seeking informed consent.
- Politics: Allocation may seem arbitrary when people with equal needs interacting regularly are assigned to different groups.
- Logistics: Sometimes, it is not practicable to randomise experimental subjects individually. In the staff training example above, training in the tools is provided at staff briefings at the beginning of each shift, making it impracticable to randomise across call centre staff within the centre.
- Cost: If you randomise at the suburb level, we usually have to treat everyone in the suburb.

17.6 Three research designs

We have discussed three aspects of the intervention that we can randomise: access, timing and encouragement.

Another dimension to consider is how we can create variation in exposure to the program. Here I discuss three: the basic lottery, a lottery around the cutoff and the phase-in design.

The basic lottery

The basic lottery randomises access to the intervention and leaves the treatment status unchanged throughout. We compare those with and without access to the intervention.

The basic lottery is most workable when a program is oversubscribed, resources are constant for the evaluation period, and it is acceptable that some receive no intervention.

Advantages are that it is familiar, understood, generally seems fair, easy to implement and allows for estimation of long-term impacts.

A disadvantage is differential attrition, as units in the control group may have little reason to cooperate with the survey.

Lottery around the cutoff

A lottery around the cutoff randomises the intervention among those close to an eligibility cutoff. This strategy is workable when eligibility is determined by a scoring system, and there are many participants.

A disadvantage of this strategy is that it measures the impact of the intervention only on those close to the eligibility cutoff.

Phase-in

The phase-in strategy randomises the timing of access and switches groups from control to treatment over time. It compares those with access to those who have not yet received access. This strategy is most workable when everyone must eventually receive the program and resources are growing over time.

An advantage of this approach is that phased roll-outs of interventions are common, and the control group may be more willing to cooperate in anticipation of future benefits.

A disadvantage is that the control group is of limited duration, meaning there is a limited time over which impact can be measured. Anticipation of the treatment may also affect the behaviour of the control group.

Question

Only 5% of people in your company are taking advantage of a new mindfulness program provided by your employer. You would like to evaluate if this program improves employee productivity.

What type of design would be suitable for this evaluation?

A phase-in design An encouragement design A lottery that would give access to the program to some employees

An encouragement design would be suitable as the program is available to everyone but not taken up.

17.7 Randomisation techniques

As we discussed earlier, randomisation provides indirect control of uncontrolled variables. It provides us with a way to infer that differences in outcomes are due to the treatments and not due to the individual characteristics of the experimental participants.

However, randomisation is not a panacea, nor is it always practical to undertake a pure randomisation. The below discusses two complications that can be involved in randomisation.

17.7.1 Performing random assignment

To perform random assignment, we need:

A list of eligible units (e.g. people, branches, schools)
The number of randomisation cells (e.g. two if you have one treatment and the control)
The allocation fraction: the proportion of the eligible units to be assigned to each group (e.g. 50%, 50%)
If feasible, initial data on the eligible units for stratification and balance

The randomisation is balanced if the mean characteristics of each group are equal. For example, each group has the same gender split. If we have data available, we can run a “balance check” to confirm that the groups that were created are balanced.

We check for balance to:

Check that the assignment was properly randomised
Confirm that as undesirable lack of balance has not been caused by chance.

Randomisation occasionally leads to a large correlation between treatments and uncontrolled nuisance variables within a trial. For example, your control and intervention groups, by chance, may end up having people with higher incomes in one group than the other, or an unbalanced mix of sexes. If you are running only a small number of trials (often only one), this lack of balance can bias your results.

The following excerpt gives an example where two groups in a field trial became unbalanced.

In 2012, we came up with a seemingly costless simple intervention: Get people to sign a tax or insurance audit form before they reported critical information (versus after, the common business practice).

We ran studies showing that when people signed an honesty declaration before reporting information, they thought about how they were honest people, and were less likely to misreport compared to when they signed after they had filled out the form. While our original set of studies found that this intervention worked in the lab and in one field experiment, we no longer believe that signing before versus after is a simple costless fix. …

In an attempt to replicate and extend our original findings, three people on our team (Kristal, Whillans and Bazerman) found no evidence for the observed effects across five studies with 4,559 participants. We brought the original team together and reran an identical lab experiment from the original paper (Experiment 1). The only thing we changed was the sample size: we had 20 times more participants per condition. And we found no difference in the amount of cheating between signing at the top of the form and signing at the bottom.

In light of these findings, we reanalyzed the field study in the original paper and became concerned with a failure of random assignment (such that the number of miles driven before the intervention was delivered was significantly different between the two groups). What we originally thought to be a reporting difference (between customers who signed at the top versus bottom of the form) now seems more likely to be a difference in actual driving behavior—not the honest or dishonest reporting of it.

Kristal et al (2020)

If the samples are not balanced, re-performing the randomisation is not considered good practice. Rather, you do stratified random assignment, or “blocking”.

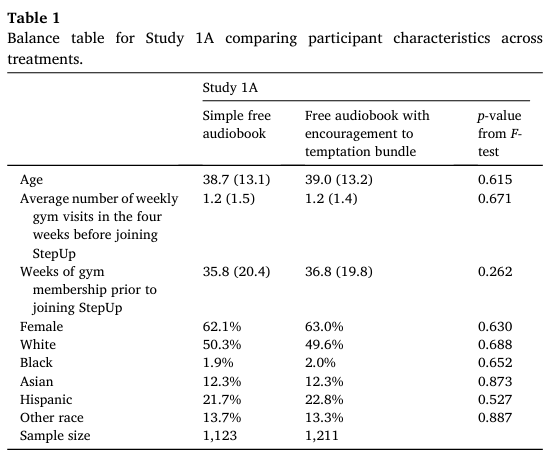
The following table is an example of a balance check from Kirgios et al (2020). The characteristics of the members of each group are compared, with a statistical test to check that there is not a statistically significant difference in these characteristics.

Of note, the more characteristics against which you check for balance, it becomes increasingly likely that you will find an unbalanced characteristic simply by chance

17.7.2 Blocking / stratification

There are experimental designs that can reduce the effect of unbalanced groups. These work by holding a set of variables constant within a subset of trials (a “block” or “strata”). These variables are often called blocking variables.

Stratified random assignment provides a way to ensure that our treatment and control groups are balanced on key variables. We first divide the pool of eligible units into strata. Within each stratum, we follow the procedure for simple random assignment.

For example, suppose we are going to test discrimination in hiring by sending CVs in response to job ads. We believe that large and small firms will respond differently. We can split the firms into two blocks, small and large, and then randomise within each of those blocks. This will balance the small and large firms across the control and intervention groups and ensure we don’t get an unbalanced experiment on that dimension.

You should stratify when:

We want to ensure balance in key characteristics (the smaller the sample size, the higher the chance that randomisation may return unbalanced groups)
We want to increase statistical power. Stratifying on variables that are strong predictors of the outcome can increase statistical power.
When we want to analyse treatment effect by subgroup.

Which stratification variables should we use?

Discrete variables (we cannot stratify on continuous variables like income and credit score, but we can create discrete groups such as income deciles)
Variables that are highly correlated with the outcome of interest. If available, the baseline value of the outcome of interest is an important stratification variable.
Variables on which we will do subgroup analysis (if we want to look at treatment effect by gender, we want balance on gender)
We do not want to stratify on too many variables, or we may find we have strata with only one or no units in them.

17.7.3 Within-subject designs

Most of the experiments we have discussed involve a “between-subject” design. The treatment and control groups comprise different subjects, with comparisons made between those subjects.

An alternative is within-subject design, whereby experimental subjects make decisions in all treatments.

Suppose we are working on increasing on-time credit card payments by sending a reminder. We might run the trial over two periods, sending a reminder to half the participants for the first payment period, and then a reminder to the other half in the second period. The control and treatment groups across the two periods are balanced as they contain the same people. This within-subjects design is called a crossover study, as participants cross over from one group to the other.

Under a within-subject design, each subject is effectively their own control, meaning that we do not need to worry about the different characteristics of decision makers. Apart from avoiding unbalanced treatment and control groups, this means there is usually less variation in treatment effects, increasing the power of the experiment.

A major disadvantage of a within-subject design is that there may be “order effects”. The intervention in one period may flow into another period. There may be effects such as fatigue. The reverse order that participants receive the treatment in a “crossover” study, such as the example above, can be used to attempt to account for these order effects, although it complicates the analysis.

Within-subject designs tend to be used where we have a limited number of experimental participants or are looking for efficiencies in the conduct of the experiment, as the design can increase power with fewer participants relative to a between-subjects design. You might also use it where you are interested in the longitudinal aspect of the interventions.

For more information, see Kirgios et al. (2020), Kristal et al. (2020), and List et al. (2011).